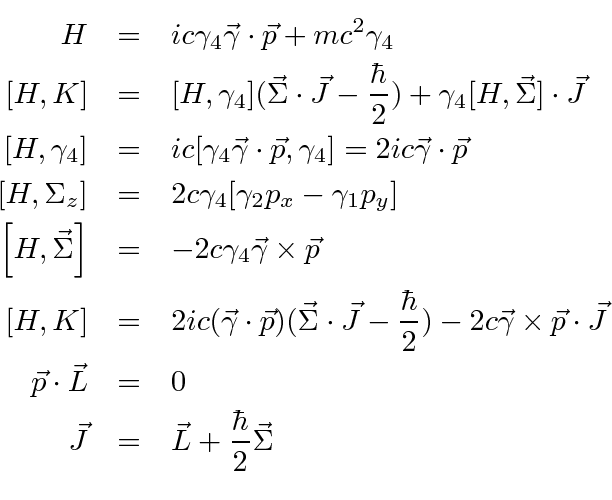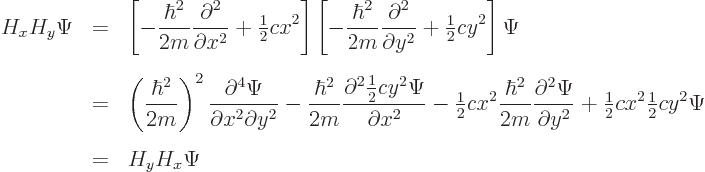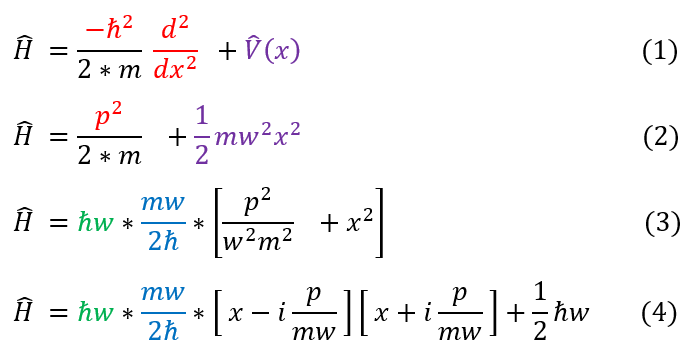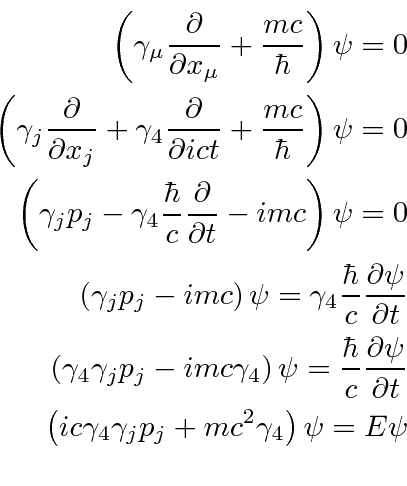Constants of the Motion for a Free Particle
Commutation and Completeness in 1D Hamiltonian
Quantum Mechanics/Operators and Commutators - Wikibooks, open books for an open world
Show that the Hamiltonian commutes with Angular momentum
commutation relation between momentum and Hamiltonian - YouTube
Solved Consider position, momentum, and the Hamiltonian as | Chegg.com
SOLVED: The Hamiltonian operator is the sum of the kinetic energy operator T and the potential energy operator V = V(r). In three dimensions, the x-component orbital angular momentum operator is given
Solved Given that the position, momentum, and total energy | Chegg.com
Topics Today Operators Commutators Operators and Commutators - ppt download
Evaluate the commutators (a) $\left[\hat{H}, \dot{p}_{a}\rig | Quizlet
Problem in time dependent hamiltonian
Solved Example 5.2. The Commutator of H and P. As an | Chegg.com
Deriving the Commutator of Exchange Operator and Hamiltonian
4.5 The Commutator
Show that (a) [x, H] = ℏip/μ (b) [[x, H], x] = ℏ^2/μ where H is the Hamiltonian. - Sarthaks eConnect | Largest Online Education Community
homework and exercises - Commutation relation for Hamiltonian for fermion and boson - Physics Stack Exchange
Quantum Mechanics/Operators and Commutators - Wikibooks, open books for an open world
Quantum Harmonic Oscillator: Ladder Operators
Commutator: Hamiltonian and position - YouTube
Angular momentum in a central potential The Hamiltonian for a particle moving in a spherically symmetric potential is ˆ H =
commutation relation between momentum and Hamiltonian - YouTube
Constants of the Motion for a Free Particle
Ehrenfest theorem - Wikipedia
